Apuntes algoritmia & python
(según valla utilizando nuevos algoritmos en ejercicios iré añadiendo mas aquí)
ÍNDICE
- SUMATORIOS
- NUMEROS PRIMOS
- CONVERION BINARIO DECIMAL
- RELLENAR DE 0000
- QUE TIPO DE VARIABLE ES
- BUSQUEDA BINARIA
- ORDENAMIENTO
- DIJKSTRA y A*
- FLOID WARSHALL
- BACKTRACKING
- KRUSCAL (ENCONTRAR ARBOLES DE EXPANSION MINIMA)
- TÉCNICAS DE RESOLUCIÓN DE PROBLEMAS
- OTRAS FORMAS DE AGILIZAR EL CÓDIGO
- OTRAS COSAS ÚTILES PARA LA OIE
SUMATORIOS
(también son útiles para números triangulares)
1 + 2 + 3 + ... + n --> x = (n * (n + 1))/2
1^2 + 2^2 + 3^2 + ... + n^2 --> x = (n * (n + 1) * (2 * n + 1))/6
1^3 + 2^3 + 3^3 + ... + n^3 --> x = ((n**2) * ((n + 1)**2))/4
1^4 + 2^4 + 3^4 + ... + n^4 --> x = (n * (n + 1) * (2 * n + 1) *(3 * (n**2) + 3 * n - 1))/30
1^5 + 2^5 + 3^5 + ... + n^5 --> x = ((n **2) * ((n + 1)**2) * (2 * (n**2) + 2 * n -1))/12
1^6 + 2^6 + 3^6 + ... + n^6 --> x = (n * (n + 1) * (2 * n + 1) * (3 * (n**4) + 6 * (n**3) - 3n + 1))/42
LISTAR NUMEROS PRIMOS
Forma lógica:
numMax == 10000 #el numero maximo que se quiere analizar, es decir, que se listaran los primos desde el numero 2 hasta ese
prime = [2, ]
for i in range(3, numMax + 1):
posPrimo= True
for uwu in range(2, int(i / 2)):
if i % uwu == 0:
posPrimo = False
break
if posPrimo:
prime.append(i)
print(prime)
Forma rapida
La función actual puede ser optimizada utilizando una técnica conocida como detección temprana de divisiones, lo que implica detener la búsqueda en cuanto se encuentre un divisor. Una forma de hacerlo es cambiar el rango en la iteración, desde 2 hasta la raiz cuadrada de n:
def primality(n):
if n <= 1:
return "Not prime"
for i in range(2, int(n**0.5) + 1):
if n % i == 0:
return "Not prime"
return "Prime"
BINARO A DECIMAL
decimal = sum(2**i for i, d in enumerate(reversed(binary_number)) if d == '1')
DECIMAL A BINARIO
binary = bin(int(decimal_number))[2:].zfill(32)
RELLENAR DE 00000
Cuando las variables que utilizamos necesitan ser de la misma longitud, por ejemplo en binario, si tenemos un número con una cantidad de dígitos menor al que necesitamos tenemos que ponerle antes 0000, es decir, si tenemos 1001 y necesitamos que tenga 8 caracteres, lo tendremos que poner así 00001001:
numeroSin0 = input("El numero:") # por ejemplo '1001'
OtoAdd = int(8 - len(numeroSin0)) # con esto calculamos cuantos 0 nos faltan
pin = str(numeroSin0.zfill(OtoAdd)) # con esto ñadimos esos 0, dejandolo en 00001001
VER QUE TIPO DE VARIABLE ES UNA VARIABLE
Si tenemos por ejemplo una raiz cuadrada y queremos ver si el output es un número entero necesitamos algun función con la que poder comprobarlo. Realmente esto se puede hacer para todo tipo de variables, pero lo voy a hacer con el ejemplo que he puesto. Para esto utilizaremos la función isinstance(x, int):
x = 4 ** 0.5
print(isinstance(x, int)) # imprime True porque la raiz cuadrada de 4 es 2, osea un número entero
x = 5 ** 0.5
print(isinstance(x, int)) # imprimer False porque la raiz cuadrada de 5 es 2,236...
BUSQUEDA BINARIA
El algoritmo de búsqueda binaria es un algoritmo de búsqueda eficiente para encontrar un elemento específico en una lista ordenada. Funciona dividiendo la lista en dos partes cada vez, comparando el elemento buscado con el elemento del medio de la lista y eliminando la mitad de la lista en la que el elemento no puede estar.
En el siguiente ejemplo a una función le metemos una lista arr y el objeto que queremos buscar x:
def binary_search(arr, x):
low = 0
high = len(arr) - 1
mid = 0
while low <= high:
mid = (high + low) // 2
# si x es mayor, ignora el lado izquierdo
if arr[mid] < x:
low = mid + 1
# si x es menor, ignora el lado derecho
elif arr[mid] > x:
high = mid - 1
# si x esta en el medio
else:
return(mid)
# If we reach here, then the element was not present
return("El elemento no esta en la lista")
ORDENAMIENTO
Hay varios algoritmos de ordenamiento, como bubble sort, insertion sort, merge sort, quick sort, entre otros. Es importante conocer al menos uno o dos de estos algoritmos y saber cómo implementarlos en Python.
BUUBLE SORT
Es un algoritmo de ordenamiento simple que repite a través de una lista de elementos varias veces, comparando elementos adyacentes y intercambiándolos si están en el orden equivocado. El proceso se repite hasta que no se realizan más intercambios, lo que indica que la lista está ordenada.
En el siguiente ejemplo, la función bubble_sort() toma una lista desordenada como input y la devuelver ordenada:
def bubble_sort(lista):
n = len(lista)
for i in range(n):
for j in range(0, n-i-1):
if lista[j] > lista[j+1]:
lista[j], lista[j+1] = lista[j+1], lista[j]
return(lista)
INSERTION SORT
El algoritmo comienza con una lista vacía en la cual se va insertando cada elemento de la lista original en orden, comparando y colocando cada elemento en su posición correcta en la lista ordenada. El proceso se repite hasta que todos los elementos del arreglo original hayan sido insertados en la lista ordenada. El tiempo de ejecución del algoritmo es O(n^2) en el peor caso, pero puede ser muy eficiente en caso de que la lista ya esté parcialmente ordenada.
def insertion_sort(arr):
# Recorremos todos los elementos del arreglo
for i in range(1, len(arr)):
# Asignamos el valor de la posición actual
key_item = arr[i]
# Asignamos el índice del elemento anterior
j = i-1
# Mientras el elemento anterior sea mayor que el elemento actual y el índice sea mayor o igual a cero
while j >=0 and key_item < arr[j] :
arr[j + 1] = arr[j]
j -= 1
# Colocamos el elemento actual en su posición correcta
arr[j + 1] = key_item
return(arr)
MERGE SORT
Merge sort es un algoritmo de ordenamiento basado en la técnica de dividir y conquistar. El algoritmo divide una lista en dos mitades, ordena cada mitad de forma independiente y luego combina las dos mitades ordenadas en una sola lista ordenada. El proceso de dividir se repite recursivamente hasta que cada mitad tenga solo un elemento, lo que significa que está ordenado. A continuación, se combinan las mitades ordenadas utilizando un proceso conocido como merge, en el cual se comparan los elementos de ambas mitades y se colocan en orden en la lista final. El algoritmo merge sort es conocido por ser estable y tener un tiempo de ejecución de O(n log n).
def merge_sort(list):
# 1. Store the length of the list
list_length = len(list)
# 2. List with length less than is already sorted
if list_length == 1:
return list
# Identify the list midpoint and partition the list into a left_partition and a right_partition
mid_point = list_length // 2
# To ensure all partitions are broken down into their individual components,
# the merge_sort function is called and a partitioned portion of the list is passed as a parameter
left_partition = merge_sort(list[:mid_point])
right_partition = merge_sort(list[mid_point:])
# The merge_sort function returns a list composed of a sorted left and right partition.
return merge(left_partition, right_partition)
# takes in two lists and returns a sorted list made up of the content within the two lists
def merge(left, right):
# Initialize an empty list output that will be populated with sorted elements.
# Initialize two variables i and j which are used pointers when iterating through the lists.
output = []
i = j = 0
# Executes the while loop if both pointers i and j are less than the length of the left and right lists
while i < len(left) and j < len(right):
# Compare the elements at every position of both lists during each iteration
if left[i] < right[j]:
# output is populated with the lesser value
output.append(left[i])
# Move pointer to the right
i += 1
else:
output.append(right[j])
j += 1
# The remnant elements are picked from the current pointer value to the end of the respective list
output.extend(left[i:])
output.extend(right[j:])
return output
arr = [38, 27, 43, 3, 9, 82, 10]
print(merge_sort(arr))
# Output: [3, 9, 10, 27, 38, 43, 82]
Esto funciona muy bien si lo que queremos es que nos devuelva la lista ordenada, pero si queremos saber el numero minimo de cambios que ha hecho para eso podemos hacerlo de esta otra forma:
def countInversions(arr):
def mergeSort(arr, temp, left, right):
inv_count = 0
if left < right:
mid = (left + right)//2
inv_count = mergeSort(arr, temp, left, mid)
inv_count += mergeSort(arr, temp, mid + 1, right)
inv_count += merge(arr, temp, left, mid, right)
return inv_count
def merge(arr, temp, left, mid, right):
i = left
j = mid + 1
k = left
inv_count = 0
while i <= mid and j <= right:
if arr[i] <= arr[j]:
temp[k] = arr[i]
i += 1
k += 1
else:
temp[k] = arr[j]
inv_count += (mid - i + 1)
j += 1
k += 1
while i <= mid:
temp[k] = arr[i]
i += 1
k += 1
while j <= right:
temp[k] = arr[j]
j += 1
k += 1
for i in range(left, right + 1):
arr[i] = temp[i]
return inv_count
n = len(arr)
temp = [0] * n
return mergeSort(arr, temp, 0, n - 1)
QUICK SORT
Este es otro algoritmo de ordenamiento de divide y vencerás. Funciona dividiendo una lista en dos sublistas, una con elementos menores que un pivote y otra con elementos mayores. Luego, se ordenan recursivamente las dos sublistas y se combinan para obtener la lista ordenada completa. El pivote se elige comúnmente como el primer, último o elemento medio de la lista. Quick sort es un algoritmo eficiente en términos de tiempo, con un tiempo de ejecución promedio de O(n log n). Sin embargo, su desempeño puede verse afectado por la elección del pivote y puede ser menos eficiente en caso de listas ya ordenadas o con muchos elementos repetidos.
def quick_sort(arr):
if len(arr) <= 1:
return arr
pivot = arr[len(arr) // 2]
left = [x for x in arr if x < pivot]
middle = [x for x in arr if x == pivot]
right = [x for x in arr if x > pivot]
return(quick_sort(left) + middle + quick_sort(right))
DIJKSTRA y A*
Es un algoritmos de búsqueda de rutas que se utiliza para encontrar la distancia minima entre dos nodos de un grafo.
import heapq
def dijkstra(graph, start, end):
heap = [(0, start)]
visited = set()
while heap:
(cost, current) = heapq.heappop(heap)
if current in visited:
continue
visited.add(current)
if current == end:
return cost
for (neighbor, weight) in graph[current].items():
if neighbor in visited:
continue
heapq.heappush(heap, (cost + weight, neighbor))
return float("inf")
graph = {
"A": {"B": 1, "C": 4},
"B": {"A": 1, "C": 2, "D": 5},
"C": {"A": 4, "B": 2, "D": 1},
"D": {"B": 5, "C": 1},
}
start = "A"
end = "D"
cost = dijkstra(graph, start, end)
OUTPUT: 3
Explicación
Este algoritmo hace distintos pasos:
1- Inicialmente, se establece la distancia desde el nodo de origen hasta sí mismo en cero, y la distancia desde el nodo de origen hasta todos los demás nodos en el grafo se establece en infinito.
2- Se selecciona el nodo con la distancia mínima que aún no ha sido visitado, y se marca como visitado.
3- Se actualiza la distancia desde el nodo de origen hasta cada uno de los vecinos del nodo seleccionado que aún no han sido visitados, utilizando la fórmula distancia_a_vecino = distancia_a_nodo_seleccionado + peso_arista.
4- Se repiten los pasos 2 y 3 hasta que se hayan visitado todos los nodos o hasta que se haya encontrado el nodo destino.
5- Finalmente, la distancia desde el nodo de origen hasta el nodo destino es la distancia más corta.
FLOID WARSHALL
Es una variante de Dijkstra que se utiliza para cuando tenemos que calcular la distancia minima entre diversos nodos de un grafo.
Claro, para eso podemos utilizar Dijkstra una y otra vez, pero se puede optimizar el tiempo y en algunos jueces puede pasar que esten los tiempos muy ajustados y en esos casos no nos sirve, por lo que tenemos que optimizarlo un poco mas.
Este otro algoritmo tiene otra ventaja a Dijkstra que es que puede trabajar con números negativos, algo que Dijkstra no puede.
El algoritmo de Floyd-Warshall se basa en el cálculo de todas las distancias mínimas entre cualquier par de nodos de un grafo con pesos. Es un algoritmo de programación dinámica que utiliza una matriz de distancias para ir actualizando los valores hasta obtener la matriz final que contiene todas las distancias mínimas. Este algoritmo es útil para resolver problemas de camino mínimo en grafos con pesos y se puede aplicar a grafos con ciclos y grafos negativos.
Para saber todas las distancias minimas entre todos los nodos:
def floyd_warshall(graph):
n = len(graph)
for k in range(n):
for i in range(n):
for j in range(n):
graph[i][j] = min(graph[i][j], graph[i][k] + graph[k][j])
return graph
Esto nos devuelve una matriz arr[nodo1][nodo2] con todas las distancias, luego solo tenemos que ir a los nodos que queramos en esa matriz.
BACKTRACKING
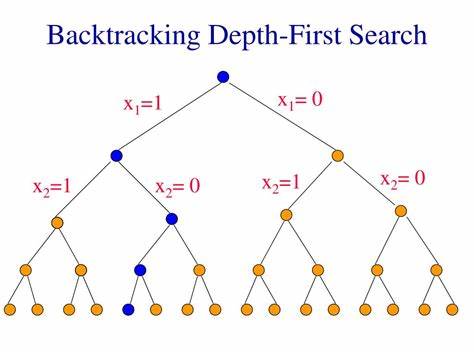
Backtracking es un algoritmo de búsqueda de soluciones que se basa en explorar una serie de soluciones posibles y retroceder en el camino si se llega a una solución inválida. Se utiliza en problemas de programación en los que se deben encontrar todas las soluciones posibles o una solución óptima en un espacio de búsqueda muy grande. Es una técnica eficiente para resolver problemas como laberintos, juegos de mesa y problemas de satisfacción de restricciones.
TEORIA (paso a paso)
(Esto lo estoy escribiendo unos cuantos dias mas tarde que los ejemplos que hay después y tras resolver problemas mas complejos como el de las n-reinas…, por lo que puede cambiar un poquito)
https://github.com/AirilMusic/Programitas/blob/main/prepOIE/Libros-de-Julia.py https://github.com/AirilMusic/Programitas/blob/main/prepOIE/N-reinas.py
Según lo que he ido aprendiendo a lo largo de los ejercicios, hay un metodo que se repite y puede facilitarte mucho el trabajo (a mi manera, sin utilizar recursiovidad), a continuación están los pasos para programar esta técnica.
1 - Encontrar los casos base, es decir, si tenemos que poner las posibles combinaciones (o las que cumplan x condición) de ["uwu", "awa", "owo"] los casos base son "uwu", "awa", "owo". (son las que tendra (arr) en la primera vuelta, osea, al inicio)
2 - Hacer un bucle que se repita la longitud maxima de las posibilidades que nos piden (en caso de que pidan todas las posibilidades con distinto número de items, simplemente en vez de borrar el array (arr) donde estemos guardadando los caos para luego añadirle los actualizados, simplemente no lo borramos y le añadimos mas, pero tenemos que tener en cuenta que si el caso que queremos añadir esta en la lista que no lo añada)
3 - Un bucle que se repita la cantidad de items de la lista (arr), para modificarlos todos
4 - Un bucle que se repita la cantidad de casos base que hay, para que a cada elemento de arr le añada (o le intente añadir) un caso base para generar otra posible combinación.
5 - Ahora dentro de este blucle es donde entran las condiciones, si no hay ninguna pues directamente añadimos al array (arr) el elemento del array que estamos utilizando + el elemento de este ultimo bucle. Sino, ponemos que solo si cumple x condición que lo añada. Para facilitarlo lo que hago es crear un segundo array (arr2) y en este meto todas las combinaciones hasta que el bucle que recorre (arr) haya dado una vuelta completa, y ahi se lo añado a (arr) o borro lo que haya y se lo añado, depende de lo que nos pidan.
6 - Y ya solo nos quedaría printear la lista (arr)
GENERAR TODAS LAS COMBINACIONES
import itertools
n = int(input())
arr = list(input().split())
out = []
for i in range(1, len(arr)+1):
c = itertools.combinations(arr, i)
for a in c:
out.append(a)
o=set(out)
for i in o:
print(' '.join(i))
GENERAR TODAS LAS PERMUTACIONES
n = int(input())
arr = []
for i in range(1, n+1):
arr.append(i)
l = len(arr)
for i in range(l):
for a in range(i+1, l):
arr[i], arr[a] = arr[a], arr[i]
print(arr)
for k in range(i+1, l):
for u in range(k+1, l):
arr[k], arr[u] = arr[u], arr[k]
print(arr)
arr[k], arr[u] = arr[u], arr[k]
arr[i], arr[a] = arr[a], arr[i]
RECORTAR RAMAS
Pero también podemos cortar ramas, es decir, que si no cumplen x requisito no se siga por ese camino, por ejemplo, eso se puede hacer con un if, un ejemplo simple es este:
m, n = map(int, input().split())
arr = list(map(int, input().split()))
pos = [0]
for i in range(n):
pos2 = []
for a in pos:
if a + arr[i] <= m:
pos2.append(a + arr[i])
if a - arr[i] >= -m:
pos2.append(a - arr[i])
pos = pos2
for p in pos:
print(p)
KURSKAL (para encontrar el árbol de expansión mínimo)
Kruskal es un algoritmo que se utiliza para encontrar el MST en un grafo no dirigido y conexo, es decir, un grafo en el que existe un camino entre cualquier par de vértices y en el que los bordes tienen pesos asociados a ellos.
Funciona así:
1- Ordenamos todas las aristas por su peso de menor a mayor
2- Para cada arista, si los nodos a los que conecta ya están conectados en el MST actual, la descartamos. De lo contrario, añadimos la arista al MST.
3- Repetimos el proceso hasta que el MST tenga n-1 aristas, donde n es el número de nodos en el grafo.
Ejemplo en python:
class Grafo:
def __init__(self, vertices):
self.V = vertices
self.grafo = []
def agregarArista(self, u, v, w):
self.grafo.append([u, v, w])
def encontrar(self, padre, i):
if padre[i] == i:
return i
return self.encontrar(padre, padre[i])
def unir(self, padre, rank, x, y):
xroot = self.encontrar(padre, x)
yroot = self.encontrar(padre, y)
if rank[xroot] < rank[yroot]:
padre[xroot] = yroot
elif rank[xroot] > rank[yroot]:
padre[yroot] = xroot
else :
padre[yroot] = xroot
rank[xroot] += 1
def Kruskal(self):
resultado =[]
i = 0
e = 0
self.grafo = sorted(self.grafo,key=lambda item: item[2])
padre = [] ; rank = []
for node in range(self.V):
padre.append(node)
rank.append(0)
while e < self.V -1 :
u,v,w = self.grafo[i]
i = i + 1
x = self.encontrar(padre, u)
y = self.encontrar(padre, v)
if x != y:
e = e + 1
resultado.append([u,v,w])
self.unir(padre, rank, x, y)
for u,v,weight in resultado:
print ("%d - %d: %d" % (u,v,weight))
g = Grafo(4)
g.agregarArista(0, 1, 10)
g.agregarArista(0, 2, 6)
g.agregarArista(0, 3, 5)
g.agregarArista(1, 3, 15)
g.agregarArista(2, 3, 4)
g.Kruskal()
TÉCNICAS DE RESOLUCIÓN DE PROBLEMAS
DIVIDE Y VENCERÁS
Es una técnica de resolución de problemas en la que un problema grande se divide en problemas más pequeños y más fáciles de resolver.
PROGRAMACIÓN DINÁMICA
Es una técnica de resolución de problemas que consiste en dividir un problema en subproblemas y almacenar las soluciones a estos subproblemas para evitar tener que volver a resolverlos.
Es muy útil utilizar funciones para esto.
GREEDY
Es una técnica de resolución de problemas en la que se toma la decisión óptima en cada paso con la esperanza de que esto lleve a una solución global óptima.
OTRAS FORMAS DE AGILIZAR EL CÓDIGO
Utilizar la función set() en vez de list()
Por ejemplo: En un problema de HR hice este código, pero es demasiado lento, por lo que habia 3 test que no superaba por tiempo:
def twoStrings(s1, s2):
l = list(s1)
m = list(s2)
b = False
if len(l) < len(m):
for i in range(len(l)):
if l[i] in m:
b = True
break
else:
for i in range(len(m)):
if m[i] in l:
b = True
break
if b == True:
return("YES")
else:
return("NO")
Por lo que para hacerlo mas rapido y simplificarlo lo hice cambiando la función list() en vez de set()`:
def twoStrings(s1, s2):
set1 = set(s1)
set2 = set(s2)
for char in set1:
if char in set2:
return "YES"
return "NO"
Y esto agilizó mucho el código.
Esto por curioso que parezca (por lo menos a mi me parecia antiintuitivo porque en los diccionarios se almacena {key}:{value} por lo que en mi lógica debería de tardar mas, pero no es así). Como ya he dicho con la función set() los conjuntos de datos se almacenan como diccionarios y con list() se almacenan como listas.
En los diccionarios, se utiliza una función de hash para asignar una clave a cada elemento, lo que permite una búsqueda rápida en tiempo constante (O(1)) en promedio. Por otro lado, en las listas, se debe recorrer cada elemento para encontrar un elemento específico, lo que lleva un tiempo de búsqueda lineal (O(n)) en promedio.
Por lo tanto, si tienes que realizar muchas operaciones de búsqueda, es más eficiente utilizar un diccionario en lugar de una lista.
Forma rapida de ordenar una lista en modo ascendente
En vez de complicaronos la vida con algoritmos que nos pueden dar problemas, podemos utilizar esta función de python:
arr = [2,1,5,4,3]
arr.sort()
# output: [1,2,3,4,5]
BISECTION
Cuando tenemos una lista muy grande y por ejemplo tenemos que hacer la media de los ultimos x números de la lista, hay que sumar todos y dividorlos por x, claro, cuando mas grande sea la lista hay que hacer muchas sumas, por lo que es muy costoso, por lo que en vez de calcular la suma de toda esa sublista, podemos quitarle el primer número y añadirle el siguiente, porque de esta forma no hacemos todas las sumas sino que es una única suma y una única resta (y luego ya hacerla división).
Para esto python tiene una herramienta que lo automatiza, es decir bisection (tambien se puede hacer de forma manual y no seria demasiado complejo, pero lo voy a explicar con bisection).
Ejemplo de código sin utilizar bisection, es decir, haciendo todas las sumas:
def activityNotifications(expenditure, d):
if len(expenditure) < d:
return(0)
else:
c = 0
fn = 0
for i in range(d):
fn += expenditure[i]
fn = int((fn/d)*2)
for i in range(d):
if expenditure[i] >= fn:
c += 1
for i in range(len(expenditure)-d):
a = i+d
sn = 0
for u in range(d):
sn += expenditure[a-u-1]
sn = int((sn/d)*2)
if expenditure[a] >= sn:
c += 1
return(c)
Ejemplo con bisection, es decir, con solamente dos operaciones (una suma y una resta):
import bisect
# Esta clase esta creada para manejar mas comodamente el append, pero se puede llamar directamente a la función bisect()
class SortedDeque:
# Se sortea el array al principio
def __init__(self, arr):
self.sorted_arr: list[int] = sorted(arr)
# Insertar el valor sin desordenar el array.
def append(self, n: int):
bisect.insort(self.sorted_arr, n)
#Encuentra la posición del valor y lo elimina
def pop_value(self, n: int):
n_index = bisect.bisect_left(self.sorted_arr, n)
self.sorted_arr.pop(n_index)
# Devuelve la mediana
def get_median(self):
length = len(self.sorted_arr)
mid = length // 2
if length % 2 == 1:
return self.sorted_arr[mid]
else:
return sum(self.sorted_arr[mid - 1: mid + 1]) / 2
# ALGORITMO
def activityNotifications(expenditure: list[int], d: int):
length = len(expenditure)
if length <= d:
return 0
out = 0
trailing_days = SortedDeque(expenditure[:d])
for ptr in range(d, length):
if ptr != d:
trailing_days.pop_value(expenditure[ptr - d - 1])
trailing_days.append(expenditure[ptr - 1])
median = trailing_days.get_median()
if expenditure[ptr] >= 2 * median:
out += 1
return out
OTRAS COSAS ÚTILES
INPUTS
caso 1
Muchas vece los inputs los dan algo así:
20 2 3
10 3 2
23 11 7
0
0 indica que el input ya se ha terminado, pero no hay que tenerlo en cuenta. Claro, esto lo tenemos que convertir en algo interpretable, porque es un string que no podemos utilizar para nada. Para eso una forma es meter todas las lineas en un array y luego en cada uno de esos sub arrays meter los items de cada linea, ejemplo [['20','2','3'],['10','3','2'],['23','11','7']] (luego ya podríamos cambiar el tipo de variable y eso):
inp = ""
arrs = []
while inp != "0":
inp = input()
if inp != "0":
arrs.append(inp.split())
print(arrs)
caso 2
En este otro caso en la primera línea nos dan las partidas que se ván a jugar, y cada partida tendrá dos líeneas como inputs. En la primera nos dan las variables (no voy a especificar para que son porque no nos importa para la explicación) S y n. Y en la siguiente linea hay n items:
2
10 6
2 7 4 3 4 8
20 1
7
Esto lo podemos agrupar en un array que tenga el número que nos dan en la primera línea. Luego dentro de cada uno de esos arrays habra otros dos que tengan las dos lineas de cada partida y dentro de esas estaran los datos [[['10', '6'], ['2', '7', '4', '3', '4', '8']], [['20', '1'], ['7']]]:
arrs = []
for i in range(int(input())):
arrs.append([input().split(),input().split()])
print(arrs)
caso 3
En este caso nos dan un input en el que la primera linea tiene las variables n y m. En la segunda nos dan un array c y luego hay m lineas de input en los que nos dan [X, Y, C] donde X = nodo1, Y = nodo2 y C = costo del camino entre los nodos. Y no se para hasta que se pone 0 0:
4 4
100 100 100 100
1 2 10
2 3 30
4 1 40
4 3 20
5 3
1000 2000 1000 1000 3000
4 5 10
1 2 20
3 2 30
0 0
Este caso es un poco mas complejo. Lo primero que tenemos que hacer es que se ejecute hasta que el input sea 0 0. Luego cada vez que se ejecuta tenemos que primero guardar las variables ny m. Y también la lista c. Y por ultimo tenemos que hacer la lista de los caminios entre nodos y sus costes, así [[X, Y, C], [X, Y, C], [X, Y, C], ...]:
inp = ""
while inp != "0 0":
inp = input()
if inp != "0 0":
n, m = [int(x) for x in list(inp.split())] #n = numero de localidades, m = numero de autopistas
c = list(input().split()) #costes un aeropuerto en la localidad [i]
a = [] #autopistas, [X,Y,C] --> X, Y son las dos localidades y C es el costo de la carretera entre ellas
for i in range(m):
a.append(list(int(x) for x in list(input().split())))
print(a)